パーセプトロンとニューラルネットワーク
「パーセプトロン」と「ニューラルネットワーク」について、簡単に説明します。
目次
パーセプトロン
パーセプトロンとは、ローゼンブラットというアメリカの研究者によって1957年に考案されたアルゴリズムです。
出典：ゼロから作るDeep Learning（オライリー・ジャパン）
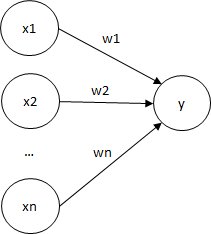
単層のパーセプトロンは以下の図のようになります。
入力信号xnに重みwnをかけて、その総和を求めます。
求めた総和が閾値θ以下の場合yは0を出力し、閾値を超える場合yは1を出力します。
$$\begin{eqnarray}
y=\left\{ \begin{array}{ll}
0 & (w_{1}x_{1}+w_{2}x_{2} \leq θ) \\
1 & (w_{1}x_{1}+w_{2}x_{2} > θ) \\
\end{array} \right.
\end{eqnarray}$$
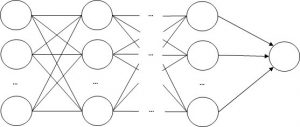
以下のように多層パーセプトロンを用いれば、より複雑な処理を行うことが出来ます。
なにが出来る？
パーセプトロンを用いると、ANDやORゲートなどの論理回路を表現することが出来ます。
2層のパーセプトロンを用いれば、XORゲートも表現できます。
（単層のパーセプトロンではXORゲートは表現できません）
ニューラルネットワーク
パーセプトロンとの違い
ニューロンのつながり方に関して言えば、前章で見たパーセプトロンと何ら変わりありません。
出典：ゼロから作るDeep Learning（オライリー・ジャパン）
ネットワークの見た目の構造に変わりはありませんが、以下のような違いがあります。
- パーセプトロンでは、出力（ノードの活性化関数）に以下のようなステップ関数を使用していました。
- ニューラルネットワークでは、例えばシグモイド関数のような滑らかな活性化関数を用います。
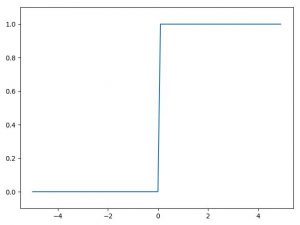
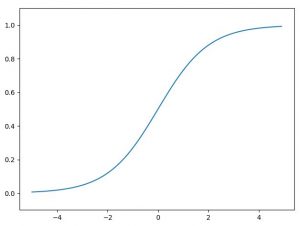
ニューラルネットワークでは、一般的に活性化関数に非線形関数を使用します。
非線形関数とは、例えば上記のステップ関数やシグモイド関数のような単純な1本の直線ではない関数のことです。
なぜ非線形関数を用いるのか？
層を増やすことの利点を生かすためです。
線形関数を用いた場合、層を重ねることの恩恵を得ることができません。
線形関数である h(x) = cx を活性化関数として、y(x) = h(h(h(x))) を行う計算を3層のネットワークに対応させて考えることにします。
この計算は、y(x) = c × c × c × x の掛け算を行いますが、同じことは y(x) = ax (ただし、a=c^3)の1回の掛け算で、つまり、隠れ層のないネットワークで表現できるのです。出典：ゼロから作るDeep Learning（オライリー・ジャパン）
まとめ（分類）
一般的には以下のように分類されます。
- パーセプトロン
- 単層かつ活性化関数がステップ関数
- ニューラルネットワーク
- 多層かつ活性化関数がシグモイド関数などの滑らかな関数
また、「多層パーセプトロン」というと以下のようなものを指すようです。
- 3つ以上のノードの層からなるパーセプトロン
- ニューラルネットワークの一分類
参考
ゼロから作るDeep Learning
Pythonで学ぶディープラーニングの理論と実装（オライリー・ジャパン）
通りすがりに失礼します。コメントは削除していただいてかまいません。
> 入力信号xnに重みxnをかけて、その総和を求めます。
もしかして、重みはwnでしょうか。。
ご指摘ありがとうございます。
重みwnに修正いたしました。
少し気になる部分があったのでコメント失礼します。
ステップ関数も非線型関数ではないでしょうか？
シグモイドを使う理由は勾配法で最適化をするためでは？
ご指摘ありがとうございます。
ステップ関数が非線形関数ではないような記述になっていたため、修正いたしました。
シグモイド関数については、使用理由の説明は割愛し「滑らかな活性化関数」という表現にしております。