Kerasを用いたLSTMでの時系列データ予測
Kerasを用いたLSTMでの時系列データ予測の例をご紹介します。
以下のサイトを参考にしています。
Time Series prediction using Recurrent Neural Networks
目次
条件
- Python 3.7.0
- Keras 2.3.1
- tensorflow 2.0.1
- pandas 0.25.3
- numpy 1.17.3
- scikit-learn 0.21.3
LSTMとは?
LSTM(long short-term memory:長短期記憶)は、長期依存性を学習できるRNNの亜種です。
LSTMはHochreiterとSchmidhuberによって最初に提案され、他の多くの研究者によって洗練されてきました。
LSTMはさまざまな問題でうまく機能し、RNNの変種の中でも最も広く使用されています。出典:直感Deep Learning Python×Kerasでアイデアを形にするレシピ
ちなみに、RNNとはリカレントニューラルネットワーク(recurrent neural network)の略であり、データ内のパターンを認識させるのに適したニューラルネットワークです。
株価の予測
時系列データの例として、日経平均株価を使用します。
日経平均株価の時系列データは、Yahoo!ファイナンスから取得しました。
使用するデータ
以下のcsvファイルを使用します。
LSTMサンプル:終値のみ使用
サンプルソース
終値を予測するよう学習を行います。
概要は以下の通りです。
- 終値のみ使用する。
- 終値を3日分遡ってシフトした値を入力とする。
- 入力および出力データは0~1の値にスケールして学習する。
- 学習後、テスト用の入力を用いて出力を求め、オリジナルスケールに戻してグラフ化する。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense, LSTM
from keras import metrics
from sklearn.preprocessing import MinMaxScaler
df = pd.read_csv('nikkei.csv', encoding="shift_jis")
L = len(df)
Y = df.iloc[:, 4] # 終値の列のみ抽出する。
Y = np.array(Y) # numpy配列に変換する。
Y = Y.reshape(-1, 1) # 行列に変換する。(配列の要素数行×1列)
X1 = Y[0:L-3, :] # 予測対象日の3日前のデータ
X2 = Y[1:L-2, :] # 予測対象日の2日前のデータ
X3 = Y[2:L-1, :] # 予測対象日の前日データ
Y = Y[3:L, :] # 予測対象日のデータ
X = np.concatenate([X1, X2, X3], axis=1) # numpy配列を結合する。
scaler = MinMaxScaler() # データを0~1の範囲にスケールするための関数。
scaler.fit(X) # スケーリングに使用する最小/最大値を計算する。
X = scaler.transform(X) # Xをを0~1の範囲にスケーリングする。
scaler1 = MinMaxScaler() # データを0~1の範囲にスケールするための関数。
scaler1.fit(Y) # スケーリングに使用する最小/最大値を計算する。
Y = scaler1.transform(Y) # Yをを0~1の範囲にスケーリングする。
X = np.reshape(X, (X.shape[0], 1, X.shape[1])) # 3次元配列に変換する。
# train, testデータを定義
X_train = X[:190, :, :]
X_test = X[190:, :, :]
Y_train = Y[:190, :]
Y_test = Y[190:, :]
model = Sequential()
model.add(LSTM(10, activation = 'tanh', input_shape = (1,3), recurrent_activation= 'hard_sigmoid'))
model.add(Dense(1))
model.compile(loss= 'mean_squared_error', optimizer = 'rmsprop', metrics=[metrics.mae])
model.fit(X_train, Y_train, epochs=100, verbose=2)
Predict = model.predict(X_test)
# オリジナルのスケールに戻す、タイムインデックスを付ける。
Y_train = scaler1.inverse_transform(Y_train)
Y_train = pd.DataFrame(Y_train)
Y_train.index = pd.to_datetime(df.iloc[3:193,0])
Y_test = scaler1.inverse_transform(Y_test)
Y_test = pd.DataFrame(Y_test)
Y_test.index = pd.to_datetime(df.iloc[193:,0])
Predict = scaler1.inverse_transform(Predict)
Predict = pd.DataFrame(Predict)
Predict.index=pd.to_datetime(df.iloc[193:,0])
plt.figure(figsize=(15,10))
plt.plot(Y_test, label = 'Test')
plt.plot(Predict, label = 'Prediction')
plt.legend(loc='best')
plt.show()
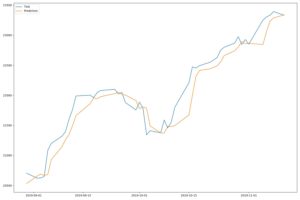
実行結果:終値のみ使用
テストデータ(青線)と比較すると、予測データ(オレンジ線)はそれほどずれてはいない感じです。
LSTMサンプル:終値、高値、安値を使用
サンプルソース
終値を予測するよう学習を行います。
先ほどの例と比較して、こちらは入力データに「高値」「安値」を追加しました。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense, LSTM
from keras import metrics
from sklearn.preprocessing import MinMaxScaler
df = pd.read_csv('nikkei.csv', encoding="shift_jis")
L = len(df)
Hi = np.array([df.iloc[:, 2]])
Low = np.array([df.iloc[:, 3]])
Close = np.array([df.iloc[:, 4]])
# 入力データ、出力データ作成
Hi = Hi.reshape(-1, 1) # 行列に変換する。(配列の要素数行×1列)
Low = Low.reshape(-1, 1) # 行列に変換する。(配列の要素数行×1列)
Close = Close.reshape(-1, 1) # 行列に変換する。(配列の要素数行×1列)
Hi1 = Hi[0:L-3, :] # 予測対象日の3日前のデータ
Low1 = Low[0:L-3, :] # 予測対象日の3日前のデータ
Close1 = Close[0:L-3, :] # 予測対象日の3日前のデータ
Hi2 = Hi[1:L-2, :] # 予測対象日の2日前のデータ
Low2 = Low[1:L-2, :] # 予測対象日の2日前のデータ
Close2 = Close[1:L-2, :] # 予測対象日の2日前のデータ
Hi3 = Hi[2:L-1, :] # 予測対象日の前日データ
Low3 = Low[2:L-1, :] # 予測対象日の前日のデータ
Close3 = Close[2:L-1, :] # 予測対象日の前日のデータ
X = np.concatenate([Low1, Hi1, Close1, Low2, Hi2, Close2, Low3, Hi3, Close3], axis=1)
Y = Close[3:L, :] # 予測対象日のデータ
scaler = MinMaxScaler()
scaler.fit(X)
X = scaler.transform(X)
scaler1 = MinMaxScaler()
scaler1.fit(Y)
Y = scaler1.transform(Y)
X = np.reshape(X, (X.shape[0], 1, X.shape[1]))
print(X.shape)
X_train = X[:190, :, :]
X_test = X[190:, :, :]
Y_train = Y[:190, :]
Y_test = Y[190:, :]
model = Sequential()
model.add(LSTM(100, activation='tanh', input_shape=(1, 9), recurrent_activation='hard_sigmoid'))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='rmsprop', metrics=[metrics.mae])
model.fit(X_train, Y_train, epochs=100, batch_size=1, verbose=2)
Predict = model.predict(X_test, verbose=1)
# オリジナルのスケールに戻す、タイムインデックスを付ける。
Y_train = scaler1.inverse_transform(Y_train)
Y_train = pd.DataFrame(Y_train)
Y_train.index = pd.to_datetime(df.iloc[3:193,0])
Y_test = scaler1.inverse_transform(Y_test)
Y_test = pd.DataFrame(Y_test)
Y_test.index = pd.to_datetime(df.iloc[193:,0])
Predict = scaler1.inverse_transform(Predict)
Predict = pd.DataFrame(Predict)
Predict.index=pd.to_datetime(df.iloc[193:,0])
plt.figure(figsize=(15,10))
plt.plot(Y_test, label = 'Test')
plt.plot(Predict, label = 'Prediction')
plt.legend(loc='best')
plt.show()
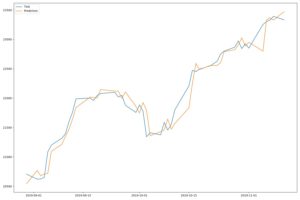
実行結果:終値、高値、安値を使用
終値のみの場合と比較して、テストデータ(青線)と予測データ(オレンジ線)の形状が似ている印象です。
しかし、騰落予測という観点ではワンテンポ遅れている感じなので微妙です。
騰落予測の精度を上げるためには、ドル円相場など日経平均株価と相関がありそうなデータを入力として使用すると良いのかもしれません。